[:en]
Abstract
We present a method for visualizing and analyzing card sorting data aiming to develop an in-depth and effective information architecture and navigation structure. One of the well-known clustering techniques for analyzing large data sets is with the k-means algorithm. However, that algorithm has yet to be widely applied to analyzing card sorting data sets to measure the similarity between cards and result displays using multidimensional scaling. The multidimensional scaling, which employs particle dynamics to the error function minimization, is a good candidate to be a computational engine for interactive card sorting data. In this paper, we apply the combination of a similarity matrix, a k-means algorithm, and multidimensional scaling to cluster and calculate an information architecture from card sorting data sets. We chose card sorting to improve an information architecture. The proposed algorithm handled the overlaps between cards in the card sorting data quite well and displayed the results in a basic layout showing all clusters and card coordinates. For outliers, the algorithm allows grouping of single cards to their closest core clusters. The algorithm handled outliers well choosing cards with the strongest similarities from the similarity matrix. We tested the clustering algorithm on real-world data sets and compared to other techniques.
The results generated clear knowledge on relevant usability issues in visualizing information architecture. The identified usability issues point to a need for a more in-depth search of design solutions that are tailored for the targeted group of people who are struggling with complicated visualizing techniques. This study is for people who need support to easily visualize information architecture from data sets.
Keywords
information architecture, card sorting, multidimensional scaling, k-means clustering algorithm, analysis, similarity matrix
Introduction
Card sorting has been proposed for designing a navigation structure for an environment that offers an interesting variety of content and functionality, such as a website (Righi et al., 2013; Capra, 2005). An effective website satisfies both the needs of stakeholders and users (Juran & Godfrey, 1998). The term card sorting applies to a wide variety of activities involving ordering, grouping, and/or naming of objects or concepts. Card sorting is one of the main methods used to improve the degree to which a website supports navigation and information retrieval (Righi et al., 2013; Rosenfeld & Morville, 2002). The information architecture (IA) is the structural design of an information space. One of the biggest challenges with website design is to create a space that users can easily and intuitively navigate to access content (Righi et al., 2013; Wurman, 1996). IA represents the underlying structures that give shape and meaning to the content and functionality of the website (Kalbach, 2007).
The current study aims to investigate and develop a clustering algorithm to analyze card sorting data sets. One of the well-known clustering techniques for analyzing large data sets is a k-means algorithm. Over the last decade it has been widely applied to study applications such as data mining with documented success (Huang, 1998; Kanungo et al., 2002; Wu et al., 2008). However, k-means has yet to be widely applied to analyze card sorting data sets to measure the similarity between cards and produce displays using multidimensional scaling. In our study, we combine a similarity matrix, a k-means algorithm, and multidimensional scaling to create an IA. We tested the new clustering algorithm in different real-world data sets and compared it to other techniques. In the presentation of the results in this paper, we used a single data source as an example.
In the following sections we start with a brief discussion of the method and similarity matrix, describe the multidimensional scaling (MDS), and discuss clustering with a brief description of the k-means algorithm. We present the results and compare the k-means algorithm with other techniques. We end by discussing overlapping and the handling of outliers.
Method
Card sorting is a data collection method that is useful for understanding users’ perceptions of relations between items. Although collecting the data is not the focus of this study, the method in which the data is collected can have an impact on how it is analyzed. Therefore, we briefly discuss the method for gathering data and discuss the analysis implications.
Card sorting uses two primary methods: a closed card sort or an open card sort. A closed card sort asks participants to sort content into predetermined categories, whereas an open card sort allows participants to sort and categorize content into their own categories and label those categories (Spencer, 2009; Spencer & Warfel, 2004; Wood & Wood, 2008). This study is based on an open card sort having been conducted. The gathering of the data can be done in an unmoderated or moderated fashion by either an online/remote or in-person study (Righi et al., 2013).
In this study, the participants were recruited at random using Amazon’s Mechanic Turk recruitment platform. The instructions were standard OptimalSort card sort instructions where all the items in the card list should be sorted into logical groups with the participant deciding what was correct. Each category needed to be named and each card could only be sorted into a single category. Category nesting was not possible. A prototype card sort analysis tool created for OptimalSort was used to generate the matrix shown in Figure 1. This matrix helps to quickly find key relationships between individual items in the card deck. We chose the data in Figure 1 as an example taken from 15 participants who submitted valid results from the total of 27 cards. These cards were related to a general banking website.
Similarity Matrix
A similarity matrix shows the relationships between cards based on counts, co-occurrence, or correlation (Righi et al., 2013). Data-gathering methods can rate the similarity of two cards or put all similar cards into the same group, or use indirect methods that list all the cards in a domain. Data from such exercises can be converted into a similarity matrix, which forms the input for analysis such as cluster analysis (see Figure 1). The similarity matrix is the key data structure in going from user data to IA. A similarity matrix creates a table with all possible pairs and counts how many participants agree with each pair. For each possible pairing of two cards in the survey, a count is provided at the corresponding point in the matrix. The count describes how many participants placed the two cards into the same category. A pair is highlighted as strong when many participants have placed the cards together. As Figure 1 shows, the strongest pair is placed in the top left corner, grouping them with the next related strongest pair that either of those cards have, and then repeats the process for that new pair. This way, clusters of cards that are strongly related to each other appear together in the same shade of blue on the matrix.
Figure 1 shows how many participants agree with each pair’s combination of cards and groups related clusters together in a color. It’s a simple tool that quickly and effectively helps to identify clusters and provides useful insight into the strength of the relationship between each pair of individual content items, and thus, how strong a group the items form (Righi et al., 2013). For example, the first column of the matrix shows that 15 people or 100% of participants put the cards “Small business advice” and “Guide to starting a business” in the same group. Looking further down that column, “Small business advice” and “Paying someone overseas” were never placing together. The algorithm was used to analyze the initial sort and produce this similarity matrix in Figure 1. The time taken to produce a similarity matrix (Figure 1) is dependent on how much data is gathered. The smaller the amount of data, the faster the algorithm works. The algorithm took 3 to 4 seconds to produce Figure 1. The results are from the 15 participants who submitted valid results from a total of 27 cards. After producing a similarity matrix using the algorithm, when you place the cursor over any cell, the two cards that the cell represents will be highlighted and will display a tooltip of those cards and the number of participants that represents the displayed percentage.
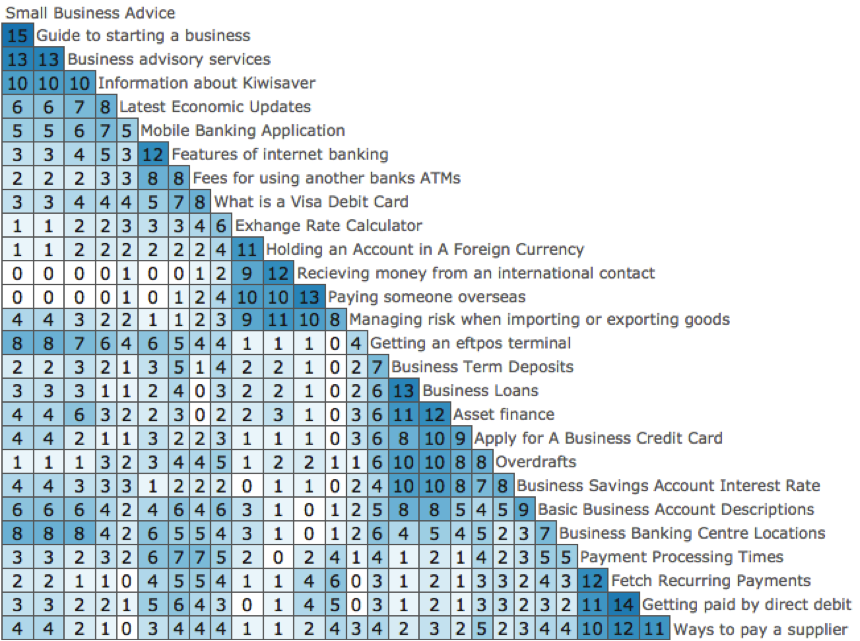
Figure 1. The similarity matrix displays how many participants agree with each pair combination of cards. The algorithm attempts to cluster similar cards along the right edge of the matrix.
In Figure 1, the dark blue color indicates cards that are located close to each other and are perceived as being similar. The white color indicates cards that are positioned far away from each other indicating a large difference in perception. (Note: The KiwiSaver is a work-based saving plan and employers play an important role. It is all about the retirement saving initiative and members are building up their savings account through regular contributions from their pay.)
In the next section, we discuss the use of multidimensional scaling (MDS) to visualize the data in Figure 1 more clearly. This method also reduces the difficulty in interpreting a plot that contains too much data, long labels, and inconsistent patterns.
Multidimensional Scaling (MDS): What MDS Can Do and How MDS Works
One of the most important goals in visualizing data is to get a sense of how near or far the points are from each other, which we can often do with a scatter plot. However, in card sorting, the data may not always come in point form at all but rather in a form of pairwise similarities or dissimilarities between cases, observations, or participants; meaning there are no points to plot. That problem leads to another difficulty in card sorting, which is how to measure and understand the relationships between cards when the underlying dimensions are not well developed or not known.
MDS is a set of methods that address all these challenges. MDS is a technique that translates a table of similarities between pairs of cards into a map where distances between the points match the similarities as much as possible (Groenen & Velden, 2014), expressing all combinations of pairs within a group of cards. The MDS technique is, therefore, important for recovering the underlying structure among the cards which are hidden behind the data. The purpose of MDS is to transform the participant judgments of similarity into distances represented in multidimensional space, resulting in the perceptual maps to show the relative positioning of all cards. Hence MDS actually moves cards around in the space defined by the requested number of dimensions and checks how well the distance cards can be reproduced by the new configuration. In more technical terms, it uses a function minimization algorithm that evaluates different configurations with the goal of maximizing the goodness of fit. MDS is a good candidate to be a methodological framework of interactive visualization. Because it allows for reconstructing the topology of an original data space defined by the similarity matrix in a target vector space, we can use it particularly in dimensions that can be explored visually (Pawliczek & Dzwinel, 2013).
When we refer to dimensions at this point, we are considering the number of coordinate axes in the multidimensional space. The position of a card in a space is specified by its coordinates on each dimension. When we use MDS, we prefer three dimensions because there is a substantial improvement over two, reducing the difficulty of interpretation. Because MDS techniques do not have any built-in procedures for labeling the dimensions, we suggest the coordinate axes as the first place to look at for the purpose of labeling dimensions. The first step is to look at the properties of the cards at each end of the dimension to determine whether there are some attributes that change in an obvious fashion. For example, using data from a sugar content study for beverages, a quick inspection will show if the beverages are arranged along a dimension in order of sugar content. If they are, the sweetness can be labelled as a dimension or at least a component of it. Additionally, we can look for clusters of points or particular patterns of a configuration. The dimensions are thought to explain the perceived similarity between items. In the case of similarities among sugar content, we expect that the reason why two beverages are seen as similar is because they have scores on the identified dimensions.
A distance matrix cannot be analyzed directly using the eigen-decomposition, but it can be transformed into an equivalent cross-product matrix that can then be analyzed. Please refer to the Appendix for more information.
Finally, we were able to plot the MDS of Figure 1 in two or three dimensions. Unfortunately, the results displayed as a single cluster; therefore, we applied the k-means algorithm to partition the cards into clusters.
Clustering
Clustering is the process of examining a collection of points and grouping the points into clusters according to some distance measure. Cluster analysis constructs good clusters when the members of a cluster have a high degree of similarity to each other and are not like members of other clusters (Estivill-Castro, 2002; Growe, 1999). In this study, we use the point-assignment algorithms. The well-known family of clustering algorithms of this type is known as the k-means (Hartigan & Wong, 1979).
K-mean Algorithms
K-means clustering is a method of cluster analysis that aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. The number of clusters is assumed to be fixed. The k-means method can cluster a large data set quickly and efficiently.
First pick points that have a good chance of lying in different clusters. There are two approaches: One idea for initializing k-means is to use a farthest-first traversal on the data set in order to pick k points that are far away from each other. However, this is too sensitive to outliers (Arai & Barakbah, 2007). The second approach clusters a sample of the data, using the method of hierarchical clustering in a Euclidean space, so there are k clusters. To start this second approach, pick a point from each cluster, perhaps the point that is closest to the centroid of the cluster. Then using the hierarchical method proceed by stages producing a sequence of partitions, each corresponding to a different number of clusters.
In this study, we chose to use the second approach that is agglomerative hierarchical clustering, meaning the groups are merged using the closest distance pair of clusters. In hierarchical clustering, given a set of N items to be clustered, and an distance matrix, the basic process of hierarchical clustering is composed of the following steps:
- Start by assigning each card to its own cluster, so that if you have N items, you now have N clusters, each containing just a single card.
- Find the closest distance pair of clusters and merge them into a single cluster, so that now you have one less cluster.
- Compute distances between the new cluster and each of the old clusters.
- Repeat steps 2 and 3 until all the single cards are clustered.
In the next section we describe options in determining when to stop the merging process and how to calculate the centroid.
Rule for Determining K Clusters
In our algorithm, we need to determine how many k clusters and how to pick the right value of k to use in k-means clustering. We have two conditions in determining when to stop the merging process and one condition determining how to calculate the centroid:
- The distance between the center points of the two clusters is shorter than the sum of the diameters of both clusters, divided by the n
- The distance between the center points of the two clusters is below some threshold.
- For each cluster, update its center by averaging all of the points that have been assigned to it.
In the first condition, we assign the starting value , that is the average of the diameters of both clusters. It’s also designed to overcome a single cluster that consists of all the cards. If this ill-condition happens, then we have to increase the value of n by 0.5 and repeat the process until we have k clusters. If the value of n repeats up to 10 times and nothing happens, we then stop the process. The second condition is designed to make sure that cards and clusters are very close together and do not satisfy the first condition. We analyzed different surveys and came up with a threshold value of 0.25.
The next step is to apply the k-means algorithm as follows:
- Place k points into the space represented by the objects that are being clustered. These points represent initial group centroids.
- Assign each card to the group that has the closest centroid.
- When all cards have been assigned, recalculate the positions of the k
- Repeat steps 2 and 3 until the centroids no longer move. This produces a separation of cards into groups from which the metric to be minimized can be calculated.
Results
We test the performance of the algorithm described above using a range of real-world data sets. The real networks allow us to observe performance under practical, real-world conditions. In order to analyze the accuracy of our proposed method, we apply k-means to analyze the same data in two ways: using k-means for three-dimensional data points (x, y and z dimensions), and two-dimensional data points (x and y dimensions).
K-Means Clustering Using Two-Dimensional Data Points
We begin by showing the performance of the algorithms using two-dimensional data points. The major part of the algorithm is based on using x and y coordinates to calculate the distances and centroids between cards and clusters. On every data set, the hierarchical algorithm was applied first to calculate the number of k clusters. Then the k-means algorithm was applied as many times as possible in the run time until the centroids of each cluster no longer moved.
To evaluate the quality of the solutions found, Table 1 shows the information architecture (IA) or clustering results from the data sets given by Figure 1. Table 1 contains five clusters, and they are not organized in any type of order or according to some type of measure. The algorithm assigned names for each category by calculating their probabilities p(name). P(name) as it approaches 1 is the most agreeable for all participants, creating names for a particular category. In Table 1, we chose two or three of the most agreeable category names. Each cluster comprises a number of cards, and the order of the cards is arranged according to their distances from similarities to dissimilarities in each category. For example, Cluster379 contains two cards named “Getting an eftpos terminal” (eftpost is an electronic funds transfer at point of sale) and “Basic Business Account Descriptions.” The two category names for Cluster379 are “Banking help” [0.29] and “Accounts” [0.25]. This approach makes it easier to compare the results with other algorithm results. We repeated the test and found that it took around 4 to 6 seconds to produce the results for the two-dimensional data points; these results are shown in Table 1 and Figure 2.
Table 1. Statistically Best IA Submissions by Participants in the Card Sort Using Two-Dimensional Data Points from the Data Sets Shown in Figure 1.
|
Cluster590 |
Cluster801 |
Cluster960 |
Cluster379 |
Cluster881 |
|
Things I might want to read once or at least not often [0.78] Business Services & News [0.67] Information & Advice [0.62] |
Helping your business tick along [0.75] Payments [0.67] Making Payments & Receiving [0.62] |
International [1.00] International business help [0.83] International Banking [0.80] |
Banking help [0.29] Accounts [0.25] |
Business Finance [1.00] Loan and Interest Rates [0.83] |
|
Small Business Advice Guide to starting a business Business advisory services Information about Kiwisaver Mobile Banking Application Features of internet banking Latest Economic Updates Business Banking Centre location
|
Payment Processing Times Fetch Recurring Payments Getting paid by direct debit Ways to pay a supplier Fees for using another banks ATMs What is a Visa Debit |
Exchange Rate Calculator Holding an Account in A Foreign Currency Receiving money from an international contact Paying someone overseas Managing risk when importing or exporting goods |
Getting an eftpos terminal Basic Business Account Descriptions |
Business Term Deposits Business Loans Asset finance Apply for a Business Credit Card Overdrafts Business Savings Account Interest Rate |
To visualize our clustering results in Table 1, we plotted the data in Figure 2. Figure 2 is designed to represent the relationships between cards in a multidimensional space. The cards are represented on a plot with Dimension 1 and Dimension 2 as axes. Dimensions are item attributes that seem to order the items in the map along a continuum. For example, an MDS of perceived similarities among breeds of dogs may show a distinct ordering of dogs by size. The ordering might go from right to left, top to bottom, or move diagonal at any angle across the map. At the same time, an independent ordering of dogs according to viciousness (or furriness, intelligence, etc.) might be observed. This ordering might be perpendicular to the size dimension or might cut a sharper angle. The underlying dimensions are thought to explain the perceived similarity between items. The relationship between the cards on the plot should represent their underlying dissimilarity. The cards that are located close to each other are perceived as being similar. In contrast, the cards that are positioned far away from each other indicate a large difference in perception. In fact, the cards closer together are more similar than those further apart. We made it clear that k-means clustering started from the partition that is obtained by hierarchical clustering for two-dimensional data points. Producing an IA of five cluster solutions in which each cluster is shown by different colors.
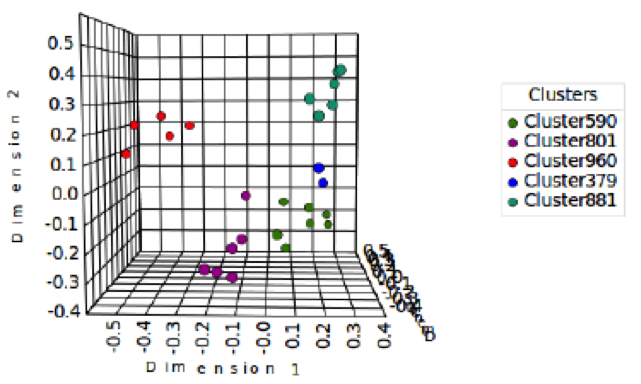
Figure 2. Multidimensional scaling of the clustering results in Table 1. Using two-dimensional data points produced a five-cluster solution with each cluster shown by different colors. Placing the cursor over any color ball point will highlight the two cards that the ball point represents.
Comparing Two- and Three-Dimensional Data Points
In order to evaluate the similarity and difference in the card sort data, we also applied k-means clustering by using three-dimensional data points to see how much the relationship between the cards and participants agreed with each other. Table 2 indicates the three-dimensional clustering results from the data shown in Figure 1. The names in each category were arranged according to their probabilities, and the cards were arranged in the order according to their distances from similarities to dissimilarities in each category. You can see that the clustering results on Table 2 have some new arrangements of cards and category names when compared to Table 1. Even though there are five k clusters, it is not of interest in card sorting. The participants agreed more with the clustering results in Table 2 than Table 1 based on the calculation of the category name probabilities. Clustering results from using two-dimensional data points produces a large number of clusters in comparison to three-dimensional data points when the number of participants and cards increases. A difference in cluster numbers illustrates the methodological issues with the choice of analysis for card sorting. We also visualize the clustering results of Table 2 in Figure 3 with each color representing a cluster. We repeated the test and found that it took around 3 to 6 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3. Note that we created our software tools to calculate and show the matrix in Figure 1. We also created our software tools to show the results in Table 1 and Figure 2.
Table 2. Best IA Submissions by Participants in the Card Sort Using Three-Dimensional Data Points from the Data Sets Given in Figure 1.
|
Cluster735 |
Cluster278 |
Cluster819 |
Cluster46 |
Cluster315 |
|
Information & Advice [1.00] Business Services & News [0.71] Useful information [0.62] |
Banking help [0.44] Accessing our Services [0.43] Administration [0.42] |
Payments [0.80] Using your accounts [0.71] Managing Payments [0.67] |
International [1.00] International business help [0.83] International Banking [0.80] |
Business Finance [1.00] Loan and Interest Rates [0.83] Helping your business grow [0.75] |
|
Business advisory services Information about Kiwisaver Guide to starting a business Small Business Advice Latest Economic Updates |
Getting an eftpos terminal Basic Business Account Descriptions Business Banking Centre Locations Features of internet banking What is a Visa Debit Card Mobile Banking Application |
Ways to pay a supplier Fees for using another banks ATMs Payment Processing Times Getting paid by direct debit Fetch Recurring Payments |
Holding an Account in A Foreign Currency Receiving money from an international contact Exchange Rate Calculator Managing risk when importing or exporting goods Paying someone overseas |
Asset finance Overdrafts Apply for A Business Credit Card Business Savings Account Interest Rate Business Term Deposits Business Loans |
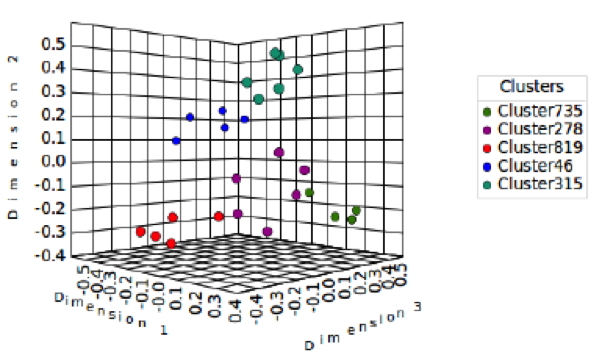
Figure 3. Multidimensional scaling of the clustering results from Table 2. Using three-dimensional data points to produce five-cluster solutions in which each cluster is shown by different colors.
To validate the current algorithm, a comparison of the results with the predictions of other techniques of card sorting is provided in the next section.
Comparing Two- and Three-Dimensional Data Points with BMM, AAM, and PCA
In order to evaluate and compare the similarity and difference in the card sort data between the current algorithm and the Participant-Centric Analysis (PCA), Actual Agreement Method (AAM), and Best Merge Method (BMM), we need to understand each of those techniques first.
AAM and BMM
Dendrograms are used to visualize the results of a hierarchical cluster analysis and may provide insights into high-level topics (Righi et al., 2013). The AAM and BMM are derived from cluster analysis, and both techniques are widely used in the industry to see the patterns of users’ card sorting. AAM and BMM dendrograms analyze the participants’ responses and provides an interpretation of how the cards were categorized. It also displays how the results are generated depending on the algorithm that is used. In general, both techniques agree that the bigger the category, the more people will disagree with it. This means, as the number of cards in a category gets larger, it is less likely that multiple participants will have created that exact combination of cards. However, while many users can agree on very small categories, this is not a very useful result. Providing the full range of viable categories along with scores allows us to make an informed compromise between practical requirements and what the participants are telling us. In this study, the dendrogram displays the results of performing a cluster analysis on the similarity matrix and displays the result in a dendrogram format. The dendrogram shows card clustering from strong to weak and left to right. Hovering over any cluster circle will show the strength of that cluster as a percentage: 100% meaning all participants grouped those cards together and 50% meaning half of the participants placed those cards in the same group.
The AAM depicts only factual relationships and provides the most useful data if over 30 participants have completed your survey. The AAM algorithm counts each instance of a complete category from every participant. Each category with a non-zero score (a real category) inherits the base score (i.e., before inheritance) of all superset categories. The category with the highest score is taken, and all conflicting categories are eliminated. This algorithm works best with a lot of participants, but it generally provides better results compared to the BMM algorithm. The scores that AAM provides tells you X% of participants agree with this grouping See Figure 4 that shows the dendrogram results from the data sets from Figure 1. We repeated the test and found that it took around 3 to 5 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.

Figure 4. The AAM dendrogram. The percentage scale is at the top of the dendrogram. The scores show X% of participants who agree with a grouping. The thicker the lines, the more cards are merged together. The results are from the 15 participants who submitted valid results from 27 cards.
The BMM algorithm dendrogram makes the most of a smaller number of completed card sorts. The BMM breaks each instance of a category from every participant down to their base pairs. The pair with the highest score is locked in. This repeats, and where the pair being locked in intersects with an existing locked category, it is agglomerated with that category. All subsets of this new category are eliminated. The scores that BMM provide tells us X% of participants who agree with parts of this grouping. Figure 5 shows the dendrogram results from the data sets given in Figure 1.
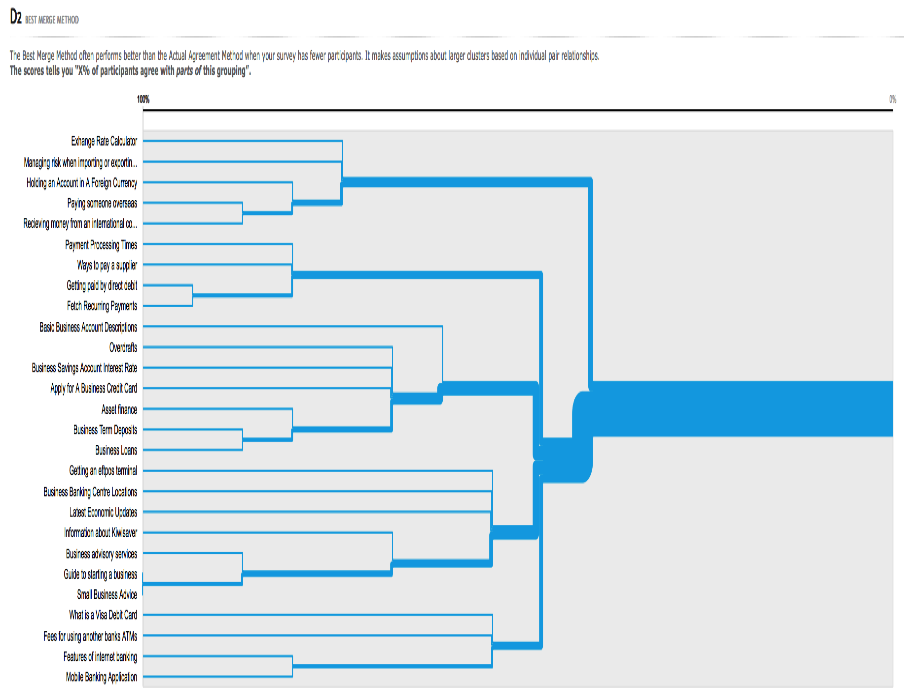
Figure 5. The BMM dendrogram. The scores show the X% of participants who agree with this grouping. The thicker the lines, the more cards are merged together. The results are from the 15 participants who submitted valid results from the total of 27 cards. We repeated the test and found that it took around 3 to 5 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.
Participant-Centric Analysis (PCA)
PCA is a new method that was developed to show an alternative display of the card sort results. At a high level, the algorithm takes every participant’s IA and compares it to every other participant’s. The more cards that are sorted into the same sorts of clusters, the more agreement one IA will have with another. Once the algorithm is completed, and the IAs have all been compared, the most popular IA with the highest agreement across all the participants is displayed; this is the largest group of participants who created similar groups. The second IA is chosen from all the participants who weren’t supporters of the first IA, and so on. It treats all the participants as IAs and treats their submitted groups as votes. Table 3 shows the most popular IA that has the highest agreement across all the participants’ results from the data sets given in Figure 1.
Table 3. PCA: Best IA—7 out of 15 Participant Card Sorts Were Similar to this IA.
|
Business Overseas |
Business Finance |
Information & Advice |
Managing Payments |
Accessing our Services |
|
International Payments International Trading Doing business overseas |
Helping your business grow Loan and Interest Rates Setting up business accounts |
Business Services & News Business basics Things I might want to read once or at least not often |
Payments Business banking transactions Making Payments & Receiving |
Business banking |
|
Business advisory services Information about Kiwisaver Guide to starting a business Small Business Advice Latest Economic Updates |
Getting an eftpos terminal Basic Business Account Descriptions Business Banking Centre Locations Features of internet banking What is a Visa Debit Card Mobile Banking Application |
Latest Economic Updates Guide to starting a business Business advisory services Information about Kiwisaver Small Business Advice |
Payment Processing Times Ways to pay a supplier Getting paid by direct debit Getting an eftpos terminal Fetch Recurring Payments |
Fees for using another banks ATMs Features of internet banking Business Banking Centre Locations Mobile Banking Application |
Note: Includes results from the 15 participants who submitted valid results from 27 cards. We repeated the test and found that it took around 3 to 6 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.
Comparison
These analyses for card sorting are chosen because all of them claim to determine a statistically optimal solution for website design. The analysis of the cards using AAM works by looking into whole clusters, rather than pairs. AAM provided better results of how participants agreed between each other, which could be transformed into meaningful steps for a website design.
In this study, we are looking for the most agreed IA. It can be seen that the AAM dendrogram result in Figure 4 provides many groups, but three of the groups contain a single card. Although many users can agree on very small categories, this is not a very useful result especially if categories are represented by a single card. Moreover, allowing a clustering algorithm to select a card that is distant from the rest of the data as an initial center, would produce poor results (Khan & Ahmad, 2004). The algorithms have direct impact on the formation of the final clusters. This can be seen with other techniques—when every cluster has at least two cards. By looking at a particular card, for example “Getting an eftpos terminal,” Figure 4 shows this as a single card in one of the group in AAM result. However, Figure 2 and 3 show that “Getting an eftpos terminal” has the coordinate (0.1815, -0.2320) in two-dimensional data points and coordinate (0.1815, -0.2320, 0.3139) in three-dimensional data points which are both close to more than one card. AAM provides more groups including groups that contain a single card when the technique uses large data sets. This will strengthen the dendrogram result to a more complex situation in order to determine the groups. The current approach discussed in this paper upgrades the results so that they are even more meaningful and easier to visualize and analyze.
The two-dimensional data points are a more likely visualization than the similarity matrix shown in the Figure 1 data. The arrangement of the cards in a cluster is more similar to what is shown along the right edge of the similarity matrix. Note that each cluster comprises the number of cards, and the order of the cards is arranged according to their distances from similarities to dissimilarities in each category. For example, Cluster881 and Cluster960 show the same arrangement of cards in each category as the similarity matrix does, which are highlighted with the dark blue color along the right edge. Cluster315 and Cluster46 in three-dimensional data points have the same number of cards and card names when compared to Cluster881 and Cluster960, but the order of the cards is varied. This is due to the calculation of the distance in three dimensions. Cluster590 in two-dimensional data points contains 8 cards as it can be seen at the top of the similarity matrix. In three-dimensional data points contains the same card names but reduced the number of cards to 5 in Cluster735. Both Cluster590 and Cluster735 contain two cards formed as a single card using the AAM algorithm as shown in Figure 4. One category in Figure 4 contains 3 cards (“Small Business Advice,” Guide to starting a business,” and “Business advisory services”) as shown in Cluster590 and Cluster735. The same category shown in Figure 4 appears further down on the similarity matrix to contain “Business Banking Center Locations.” This category arrangement does present some doubt about the efficacy of the AAM algorithm. The two single cards are next to this cluster and contain more agreements by participants. It can be seen that “Small Business Advice,” Guide to starting a business,” “Business advisory services,” “Information about Kiwisaver,” and “Latest Economic Updates” should be clustered together in Figure 1 as shown by the agreement in the two- and three-dimensional data points.
BMM is a technique based upon similarity matrixes. The limitation of BMM only works by merging the pairs, so it will be impossible to reconstruct this reduction. If we apply the threshold of 50% agreement to Figure 5, then we have five groups. Let’s compare one of the groups that contains similar cards as shown in Figure 5, Table 1, and Table 2. For example, Table 4 shows the result from one of the groups in Figure 5. This shows that five cards in Table 4 also appear in the category name “Information & Advice” in Table 2. The other two cards “Business Banking Centre Locations” and “Getting an eftpos terminal” in Table 4 are grouped differently in Table 2. To understand why the current algorithm clustered the two cards differently, we plot the result of Table 2 in Figure 6 viewing Dimension 3 as a function of Dimension 2. The green color circles in Figure 6 and 3 are the cards that contains in both BMM and k-mean algorithm for three-dimensional data points. Figure 6 shows “Business Banking Centre Locations” (0.1673, -0.1253, 0.0733) and “Getting an eftpos terminal” (0.2230, -0.0226, 0.0583) are both closer to the violet colored cluster than the green colored cluster. In two-dimensional data points, Table 1 shows that it contains all the cards in Table 4 in one cluster except one card “Getting an eftpos terminal.” In Figure 2, “Getting an eftpos terminal” is closer to another card than the rest of the cards in Table 4. This analysis indicates that the current approach can overcome the limitation of BMM by allowing the cards to reconstruct after a cluster is formed.
Table 4. One Group from Figure 5
|
Small Business Advice Guide to starting a business Business advisory services Information about Kiwisaver Latest Economic Updates Business Banking Centre Locations Getting an eftpos terminal |
The BMM method is known to work well with small sets of data, and it appears that BMM is driven well with two- and three-dimensional data points of data less than 30. Most of the categories in BMM contain cards similar to two- and three-dimensional data points categories more than in AAM categories. It can be seen that Cluster960 in two-dimensional data points and Cluster46 in three-dimensional data points have the same number of cards and card names with one category in BMM dendrogram in Figure 5. Figure 5 shows when the pair with the highest score is locked in, it will be impossible to reconstruct this reduction. This limitation is overwhelmed by two- and three-dimensional data points shown in Table 1 and 2. The card is arranged according to their distances from similarities to dissimilarities in each category.
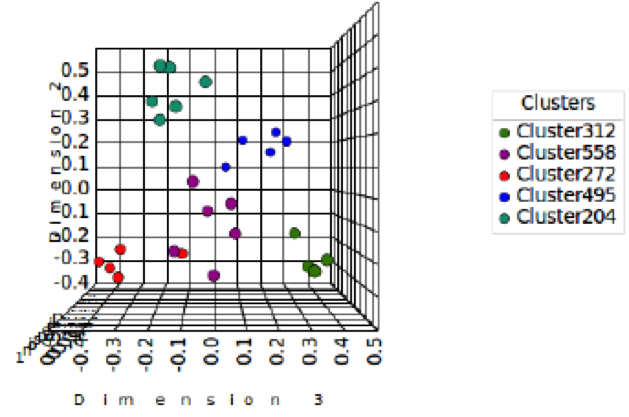
Figure 6. Multidimensional scaling of the clustering results from Table 2 viewing from Dimension 2 against Dimension 3. Using three-dimensional data points, we produced a five-cluster solution in which each cluster is shown by different colors.
The result of two techniques (k-means algorithm and PCA) reveals that PCA results (Table 3) and three-dimension data points clustering results (Table 2) have more cards in the categories that are commonly compared to two-dimension data points clustering results (Table 1). The PCA best IA is chosen depending on the highest agreement across all the participants. This technique is understood to have weakness when the number of participants is small. For example, if a survey contains four participants, the PCA algorithm takes every participant’s IA and compares it to every other participant’s. If there is less agreement between the IAs then there is no popular IA that has the highest agreement across all the participants. The current algorithm overcomes this limitation and contributes to providing better and more meaningful results if a survey uses a small number of participants. Our approach can be easily used by any practitioners whether they are not familiar with MDS. They will only need to submit the data and leave it to the software to give the results.
The next section describes how the current algorithms handle overlapping and outliers.
Overlapping and Outliers
K-means algorithm uses two- and three-dimensional data points that are able to handle the overlaps quite well. Figures 2 and 3 show only 26 cards from the total of 27. The missing card is placed at the same position with another card. This is an overlap. We displayed the results in the basic layout showing all clusters and every card’s coordinates. The basic layout shows that two cards (“Small Business Advice” and “Guide to starting a business”) have the same coordinate of (0.26053, -0.23871, 0.32583). Observations of some data sets also show that some single cards are relatively distant from the rest of the data, known as outliers. In iterative clustering algorithms, the procedure adopted for choosing initial centers has a direct impact on the formation of final clusters. Our proposed algorithm allows the grouping of single cards with their closest core clusters treating outliers by choosing the strongest similarity cards from the similarity matrix. In future work, we may explore setting a threshold for this value. We also need to test and analyzes this approach in data for more than 50 cards and do more tests to overcome the limitation of the number of cards.
Conclusion
We have considered the combination of similarity matrix, k-means algorithm, and multidimensional scaling to cluster and calculate the most agreeable information architecture in card sorting data sets. The algorithm is applicable to any card sorting data sets, and it upgrades the results so they are meaningful and easier to visualize and analyze. We found that the participants’ card sorts agreed more with the clustering results when using the three-dimensional data points than the two-dimensional, based on the calculation of the category name probabilities.
The AAM dendrogram results provide many groups and contain categories with a single card. Although many users can agree on very small categories, this is not a very useful result especially if categories are represented by a single card. Moreover, allowing a clustering algorithm to select a card that is distant from the rest of the data as an initial center, would produce poor results. The algorithms will have direct impact on the formation of final clusters. Also the results analysis indicates that the current approach can overcome the limitation of BMM by allowing the cards to reconstruct after a cluster is formed. For PCA, the current algorithm contributes to providing better and more meaningful results if the survey uses a small number of participants. This method can work well in small card sorts of those less than 30 cards. Also, we will look very closely to the analysis cards of more than 30 and up to 100 cards. Our approach is also able to handle the overlaps and outliers quite well. The proposed clustering algorithms have been tested on real-world data sets and compared to other techniques.
Tips for UX Practitioners
The following are suggestions that UX practitioners can use in their own card sorting analysis:
- Use online card sorting tools to more easily convert data into a similarity matrix. The strongest pair is placed in the top left corner, grouping them with the next related strongest pair that either of those cards have, and then repeats the process for that new pair. This way, the algorithm attempts to cluster similar cards along the right edge of the matrix. Be careful if the similarity matrix presents both the upper and lower triangular together.
- Although most online tools do not provide the capability for users to group items into subcategories, this does not imply that this decision is any less important or should be varnished over quickly. The dendrogram provided in online tools can help you more easily make decisions about where large categories naturally break into subcategories.
- Save images while analyzing data especially during the rotation in three-dimensional images. These images are useful for future presentations, illustration of results, and for making decisions during the creation of information architecture.
- It is very important to look closely at the similarity matrix and compare with two- and three-dimensional data points. At the same time look at the AAM and the BBM results.
- Do not let the length or complexity of this process discourage you from performing it. Creating an IA is a critically important step in the design of a website or application. It forms the foundation of the user’s navigation experience. Time spent on ensuring the structure is as good as you can make it, based on user input, is time well spent.
- Do not be discourage if a card is not present at the MDS display. This shows that the overlapping process has occurred. You would know that these cards are placed together by clicking on each point or by looking at the coordinates display.
- This new methodology can be used by anyone, but those who will find it the most beneficial are when they have found that other methods produce hard to read results in the form of diagram. This new methodology can give the final result in groups, and also show a visualization of the results in two- and three-dimensions.
Acknowledgments
The authors are especially indebted to Andrew Mayfield and Keith Ng for the many valuable discussions of the problems to which the above results pertain. We also thank Optimal Workshop (http://www.optimalworkshop.com) for allowing this work to use their data and algorithms.
References
Abdi, H. (2007). Metric multidimensional scaling. In N. Salkind (Ed.), Encyclopedia of Measurement and Statistics (pp. 598–605). Thousand Oaks, CA, USA: Sage.
Arai, K., & Barakbah, A. R. (2007). Hierarchical k-means: An algorithm for centroids initialization for K-means. Reports of the Faculty of Science and Engineering, 36(1), 25–31.
Baker, K. (2005). Singular value decomposition tutorial. The Ohio State University.
Berry, M. W., Dumais, S. T., & Letsche, T. A. (1995). Computational methods for intelligent information access. In Proceedings of the 1995 ACM/ IEEE Supercomputing Conference, 1995.
Capra, M.G. (2005), Factor analysis of card sort data: An alternative to hierarchical cluster analysis, Proceedings of the Human Factors and Ergonomics Society 49th Annual Meeting, HFES 2005 (pp. 91–95). Santa Monica, CA: Human Factors an Ergonomics Society Inc.
Estivill-Castro, V. (2002). Why so many clustering algorithms: A position paper. ACM SIGKDD Explorations Newsletter, 4(1), 65–75.
Groenen, P. J., & Velden, M. (2014). Multidimensional scaling. John Wiley & Sons, Ltd.
Growe, G. A. (1999). Comparing algorithms and clustering data: Components of the data mining process (Doctoral dissertation, Grand Valley State University).
Hartigan, J. A., & Wong, M. A. (1979). Algorithm AS 136: A k-means clustering algorithm. Applied statistics, 28(1), 100–108.
Huang, Z. (1998). Extensions to the k-means algorithm for clustering large data sets with categorical values. Data mining and knowledge discovery, 2(3), 283–304.
Juran, J. M., & Godfrey, A. (1998). Quality control handbook. New York, NY: McGraw-Hill.
Kalbach, J. (2007). Designing web navigation: Optimizing the user experience. O’Reilly Media, Inc.
Kanungo, T., Mount, D. M., Netanyahu, N. S., Piatko, C. D., Silverman, R., & Wu, A. Y. (2002). An efficient k-means clustering algorithm: Analysis and implementation. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 24(7), 881–892.
Khan, S. S., & Ahmad, A. (2004). Cluster center initialization algorithm for K-means clustering. Pattern recognition letters, 25(11), 1293-1302.
Pawliczek, P., & Dzwinel, W. (2013). Interactive data mining by using multidimensional scaling. Procedia Computer Science, 18, 40–49.
Righi, C., James, J., Beasley, M., Day, D. L., Fox, J. E., Gieber, J., & Ruby, L. (2013). Card sort analysis best practices. Journal of Usability Studies, 8(3), 69–89.
Rosenfeld, L., & Morville, P. (2002). Information architecture for the world wide web. O’Reilly Media, Inc.
Spencer, D. (2009) Card sorting. Designing usable categories. Brooklyn, NY, USA: Rosenfeld Media.
Spencer, D., & Warfel, T. (2004, April 7). Card sorting: A definitive guide. Boxes and Arrows. Retrieved from http://boxesandarrows.com/card-sorting-a-definitive-guide/
Steward, G. (1993). On the early history of the singular value decomposition. SIAM Review, 25(4), 551–566.
Wood, J., & Wood, L. (2008). Card sorting: Current practices and beyond. Journal of Usability Studies, 4(1), 1–6.
Wu, X., Kumar, V., Quinlan, J. R., Ghosh, J., Yang, Q., Motoda, H., & Steinberg, D. (2008). Top 10 algorithms in data mining. Knowledge and Information Systems, 14(1), 1–37.
Wurman, R. S. (1996). Information Architects. Zurich, Switzerland: Graphis Inc.
Appendix: Transforming a Distance Matrix into a Cross-Product Matrix
In this approach, dissimilarities are treated as distances in space, and they must follow the rules that govern metric distance between cards. Specifically, the dissimilarity function d assigns to every pair of cards A and B a nonnegative number according to the following three axioms:
- d(A,B) ≥ d(A,A) = 0 is the dissimilarity between two cards is greater than or equal to the dissimilarity between a card and itself, which is zero;
- d(A,B) = d(B,A) is the dissimilarity of A to B is the same as the dissimilarity of B to A;
- d(A,B) + d(B,C) ≥ d(A,C) A and C cannot be farther apart in similarity space than the sum of their distances to any other object B.
If s is the similarity measure shown in Figure 1 that later ranges between 0 and 1 by normalizing using
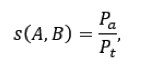
where is the number of participants that agree with each pair and the total number of participants. Then the corresponding dissimilarity measure can be defined as
![]()
In order to transform a distance matrix into a cross-product matrix, we use the approaches proposed by Abdi (2007), and the equation can be expressed in matrix form as:
![]()
where I is an identity matrix, U is an n by n matrix consisting entirely of 1s only and D is the distance matrix derived using Equation (1). The eigen-decomposition of this matrix gives
![]()
with and is the diagonal matrix of eigenvalues. Equation (3) is always achievable if we’re working with square symmetric matrix and we split into then Equation (3) becomes
![]()
One factoring technique we can use is called singular value decomposition (SUV; Baker, 2005; Berry, Dumais, & Letsche, 1995). As it turns out, the orthogonalization of a square symmetric matrix is a special case of SVD (Steward, 1993).
[:de]
Abstract
We present a method for visualizing and analyzing card sorting data aiming to develop an in-depth and effective information architecture and navigation structure. One of the well-known clustering techniques for analyzing large data sets is with the k-means algorithm. However, that algorithm has yet to be widely applied to analyzing card sorting data sets to measure the similarity between cards and result displays using multidimensional scaling. The multidimensional scaling, which employs particle dynamics to the error function minimization, is a good candidate to be a computational engine for interactive card sorting data. In this paper, we apply the combination of a similarity matrix, a k-means algorithm, and multidimensional scaling to cluster and calculate an information architecture from card sorting data sets. We chose card sorting to improve an information architecture. The proposed algorithm handled the overlaps between cards in the card sorting data quite well and displayed the results in a basic layout showing all clusters and card coordinates. For outliers, the algorithm allows grouping of single cards to their closest core clusters. The algorithm handled outliers well choosing cards with the strongest similarities from the similarity matrix. We tested the clustering algorithm on real-world data sets and compared to other techniques.
The results generated clear knowledge on relevant usability issues in visualizing information architecture. The identified usability issues point to a need for a more in-depth search of design solutions that are tailored for the targeted group of people who are struggling with complicated visualizing techniques. This study is for people who need support to easily visualize information architecture from data sets.
Keywords
information architecture, card sorting, multidimensional scaling, k-means clustering algorithm, analysis, similarity matrix
Introduction
Card sorting has been proposed for designing a navigation structure for an environment that offers an interesting variety of content and functionality, such as a website (Righi et al., 2013; Capra, 2005). An effective website satisfies both the needs of stakeholders and users (Juran & Godfrey, 1998). The term card sorting applies to a wide variety of activities involving ordering, grouping, and/or naming of objects or concepts. Card sorting is one of the main methods used to improve the degree to which a website supports navigation and information retrieval (Righi et al., 2013; Rosenfeld & Morville, 2002). The information architecture (IA) is the structural design of an information space. One of the biggest challenges with website design is to create a space that users can easily and intuitively navigate to access content (Righi et al., 2013; Wurman, 1996). IA represents the underlying structures that give shape and meaning to the content and functionality of the website (Kalbach, 2007).
The current study aims to investigate and develop a clustering algorithm to analyze card sorting data sets. One of the well-known clustering techniques for analyzing large data sets is a k-means algorithm. Over the last decade it has been widely applied to study applications such as data mining with documented success (Huang, 1998; Kanungo et al., 2002; Wu et al., 2008). However, k-means has yet to be widely applied to analyze card sorting data sets to measure the similarity between cards and produce displays using multidimensional scaling. In our study, we combine a similarity matrix, a k-means algorithm, and multidimensional scaling to create an IA. We tested the new clustering algorithm in different real-world data sets and compared it to other techniques. In the presentation of the results in this paper, we used a single data source as an example.
In the following sections we start with a brief discussion of the method and similarity matrix, describe the multidimensional scaling (MDS), and discuss clustering with a brief description of the k-means algorithm. We present the results and compare the k-means algorithm with other techniques. We end by discussing overlapping and the handling of outliers.
Method
Card sorting is a data collection method that is useful for understanding users’ perceptions of relations between items. Although collecting the data is not the focus of this study, the method in which the data is collected can have an impact on how it is analyzed. Therefore, we briefly discuss the method for gathering data and discuss the analysis implications.
Card sorting uses two primary methods: a closed card sort or an open card sort. A closed card sort asks participants to sort content into predetermined categories, whereas an open card sort allows participants to sort and categorize content into their own categories and label those categories (Spencer, 2009; Spencer & Warfel, 2004; Wood & Wood, 2008). This study is based on an open card sort having been conducted. The gathering of the data can be done in an unmoderated or moderated fashion by either an online/remote or in-person study (Righi et al., 2013).
In this study, the participants were recruited at random using Amazon’s Mechanic Turk recruitment platform. The instructions were standard OptimalSort card sort instructions where all the items in the card list should be sorted into logical groups with the participant deciding what was correct. Each category needed to be named and each card could only be sorted into a single category. Category nesting was not possible. A prototype card sort analysis tool created for OptimalSort was used to generate the matrix shown in Figure 1. This matrix helps to quickly find key relationships between individual items in the card deck. We chose the data in Figure 1 as an example taken from 15 participants who submitted valid results from the total of 27 cards. These cards were related to a general banking website.
Similarity Matrix
A similarity matrix shows the relationships between cards based on counts, co-occurrence, or correlation (Righi et al., 2013). Data-gathering methods can rate the similarity of two cards or put all similar cards into the same group, or use indirect methods that list all the cards in a domain. Data from such exercises can be converted into a similarity matrix, which forms the input for analysis such as cluster analysis (see Figure 1). The similarity matrix is the key data structure in going from user data to IA. A similarity matrix creates a table with all possible pairs and counts how many participants agree with each pair. For each possible pairing of two cards in the survey, a count is provided at the corresponding point in the matrix. The count describes how many participants placed the two cards into the same category. A pair is highlighted as strong when many participants have placed the cards together. As Figure 1 shows, the strongest pair is placed in the top left corner, grouping them with the next related strongest pair that either of those cards have, and then repeats the process for that new pair. This way, clusters of cards that are strongly related to each other appear together in the same shade of blue on the matrix.
Figure 1 shows how many participants agree with each pair’s combination of cards and groups related clusters together in a color. It’s a simple tool that quickly and effectively helps to identify clusters and provides useful insight into the strength of the relationship between each pair of individual content items, and thus, how strong a group the items form (Righi et al., 2013). For example, the first column of the matrix shows that 15 people or 100% of participants put the cards “Small business advice” and “Guide to starting a business” in the same group. Looking further down that column, “Small business advice” and “Paying someone overseas” were never placing together. The algorithm was used to analyze the initial sort and produce this similarity matrix in Figure 1. The time taken to produce a similarity matrix (Figure 1) is dependent on how much data is gathered. The smaller the amount of data, the faster the algorithm works. The algorithm took 3 to 4 seconds to produce Figure 1. The results are from the 15 participants who submitted valid results from a total of 27 cards. After producing a similarity matrix using the algorithm, when you place the cursor over any cell, the two cards that the cell represents will be highlighted and will display a tooltip of those cards and the number of participants that represents the displayed percentage.

Figure 1. The similarity matrix displays how many participants agree with each pair combination of cards. The algorithm attempts to cluster similar cards along the right edge of the matrix.
In Figure 1, the dark blue color indicates cards that are located close to each other and are perceived as being similar. The white color indicates cards that are positioned far away from each other indicating a large difference in perception. (Note: The KiwiSaver is a work-based saving plan and employers play an important role. It is all about the retirement saving initiative and members are building up their savings account through regular contributions from their pay.)
In the next section, we discuss the use of multidimensional scaling (MDS) to visualize the data in Figure 1 more clearly. This method also reduces the difficulty in interpreting a plot that contains too much data, long labels, and inconsistent patterns.
Multidimensional Scaling (MDS): What MDS Can Do and How MDS Works
One of the most important goals in visualizing data is to get a sense of how near or far the points are from each other, which we can often do with a scatter plot. However, in card sorting, the data may not always come in point form at all but rather in a form of pairwise similarities or dissimilarities between cases, observations, or participants; meaning there are no points to plot. That problem leads to another difficulty in card sorting, which is how to measure and understand the relationships between cards when the underlying dimensions are not well developed or not known.
MDS is a set of methods that address all these challenges. MDS is a technique that translates a table of similarities between pairs of cards into a map where distances between the points match the similarities as much as possible (Groenen & Velden, 2014), expressing all combinations of pairs within a group of cards. The MDS technique is, therefore, important for recovering the underlying structure among the cards which are hidden behind the data. The purpose of MDS is to transform the participant judgments of similarity into distances represented in multidimensional space, resulting in the perceptual maps to show the relative positioning of all cards. Hence MDS actually moves cards around in the space defined by the requested number of dimensions and checks how well the distance cards can be reproduced by the new configuration. In more technical terms, it uses a function minimization algorithm that evaluates different configurations with the goal of maximizing the goodness of fit. MDS is a good candidate to be a methodological framework of interactive visualization. Because it allows for reconstructing the topology of an original data space defined by the similarity matrix in a target vector space, we can use it particularly in dimensions that can be explored visually (Pawliczek & Dzwinel, 2013).
When we refer to dimensions at this point, we are considering the number of coordinate axes in the multidimensional space. The position of a card in a space is specified by its coordinates on each dimension. When we use MDS, we prefer three dimensions because there is a substantial improvement over two, reducing the difficulty of interpretation. Because MDS techniques do not have any built-in procedures for labeling the dimensions, we suggest the coordinate axes as the first place to look at for the purpose of labeling dimensions. The first step is to look at the properties of the cards at each end of the dimension to determine whether there are some attributes that change in an obvious fashion. For example, using data from a sugar content study for beverages, a quick inspection will show if the beverages are arranged along a dimension in order of sugar content. If they are, the sweetness can be labelled as a dimension or at least a component of it. Additionally, we can look for clusters of points or particular patterns of a configuration. The dimensions are thought to explain the perceived similarity between items. In the case of similarities among sugar content, we expect that the reason why two beverages are seen as similar is because they have scores on the identified dimensions.
A distance matrix cannot be analyzed directly using the eigen-decomposition, but it can be transformed into an equivalent cross-product matrix that can then be analyzed. Please refer to the Appendix for more information.
Finally, we were able to plot the MDS of Figure 1 in two or three dimensions. Unfortunately, the results displayed as a single cluster; therefore, we applied the k-means algorithm to partition the cards into clusters.
Clustering
Clustering is the process of examining a collection of points and grouping the points into clusters according to some distance measure. Cluster analysis constructs good clusters when the members of a cluster have a high degree of similarity to each other and are not like members of other clusters (Estivill-Castro, 2002; Growe, 1999). In this study, we use the point-assignment algorithms. The well-known family of clustering algorithms of this type is known as the k-means (Hartigan & Wong, 1979).
K-mean Algorithms
K-means clustering is a method of cluster analysis that aims to partition n observations into k clusters in which each observation belongs to the cluster with the nearest mean. The number of clusters is assumed to be fixed. The k-means method can cluster a large data set quickly and efficiently.
First pick points that have a good chance of lying in different clusters. There are two approaches: One idea for initializing k-means is to use a farthest-first traversal on the data set in order to pick k points that are far away from each other. However, this is too sensitive to outliers (Arai & Barakbah, 2007). The second approach clusters a sample of the data, using the method of hierarchical clustering in a Euclidean space, so there are k clusters. To start this second approach, pick a point from each cluster, perhaps the point that is closest to the centroid of the cluster. Then using the hierarchical method proceed by stages producing a sequence of partitions, each corresponding to a different number of clusters.
In this study, we chose to use the second approach that is agglomerative hierarchical clustering, meaning the groups are merged using the closest distance pair of clusters. In hierarchical clustering, given a set of N items to be clustered, and an distance matrix, the basic process of hierarchical clustering is composed of the following steps:
- Start by assigning each card to its own cluster, so that if you have N items, you now have N clusters, each containing just a single card.
- Find the closest distance pair of clusters and merge them into a single cluster, so that now you have one less cluster.
- Compute distances between the new cluster and each of the old clusters.
- Repeat steps 2 and 3 until all the single cards are clustered.
In the next section we describe options in determining when to stop the merging process and how to calculate the centroid.
Rule for Determining K Clusters
In our algorithm, we need to determine how many k clusters and how to pick the right value of k to use in k-means clustering. We have two conditions in determining when to stop the merging process and one condition determining how to calculate the centroid:
- The distance between the center points of the two clusters is shorter than the sum of the diameters of both clusters, divided by the n
- The distance between the center points of the two clusters is below some threshold.
- For each cluster, update its center by averaging all of the points that have been assigned to it.
In the first condition, we assign the starting value , that is the average of the diameters of both clusters. It’s also designed to overcome a single cluster that consists of all the cards. If this ill-condition happens, then we have to increase the value of n by 0.5 and repeat the process until we have k clusters. If the value of n repeats up to 10 times and nothing happens, we then stop the process. The second condition is designed to make sure that cards and clusters are very close together and do not satisfy the first condition. We analyzed different surveys and came up with a threshold value of 0.25.
The next step is to apply the k-means algorithm as follows:
- Place k points into the space represented by the objects that are being clustered. These points represent initial group centroids.
- Assign each card to the group that has the closest centroid.
- When all cards have been assigned, recalculate the positions of the k
- Repeat steps 2 and 3 until the centroids no longer move. This produces a separation of cards into groups from which the metric to be minimized can be calculated.
Results
We test the performance of the algorithm described above using a range of real-world data sets. The real networks allow us to observe performance under practical, real-world conditions. In order to analyze the accuracy of our proposed method, we apply k-means to analyze the same data in two ways: using k-means for three-dimensional data points (x, y and z dimensions), and two-dimensional data points (x and y dimensions).
K-Means Clustering Using Two-Dimensional Data Points
We begin by showing the performance of the algorithms using two-dimensional data points. The major part of the algorithm is based on using x and y coordinates to calculate the distances and centroids between cards and clusters. On every data set, the hierarchical algorithm was applied first to calculate the number of k clusters. Then the k-means algorithm was applied as many times as possible in the run time until the centroids of each cluster no longer moved.
To evaluate the quality of the solutions found, Table 1 shows the information architecture (IA) or clustering results from the data sets given by Figure 1. Table 1 contains five clusters, and they are not organized in any type of order or according to some type of measure. The algorithm assigned names for each category by calculating their probabilities p(name). P(name) as it approaches 1 is the most agreeable for all participants, creating names for a particular category. In Table 1, we chose two or three of the most agreeable category names. Each cluster comprises a number of cards, and the order of the cards is arranged according to their distances from similarities to dissimilarities in each category. For example, Cluster379 contains two cards named “Getting an eftpos terminal” (eftpost is an electronic funds transfer at point of sale) and “Basic Business Account Descriptions.” The two category names for Cluster379 are “Banking help” [0.29] and “Accounts” [0.25]. This approach makes it easier to compare the results with other algorithm results. We repeated the test and found that it took around 4 to 6 seconds to produce the results for the two-dimensional data points; these results are shown in Table 1 and Figure 2.
Table 1. Statistically Best IA Submissions by Participants in the Card Sort Using Two-Dimensional Data Points from the Data Sets Shown in Figure 1.
|
Cluster590 |
Cluster801 |
Cluster960 |
Cluster379 |
Cluster881 |
|
Things I might want to read once or at least not often [0.78] Business Services & News [0.67] Information & Advice [0.62] |
Helping your business tick along [0.75] Payments [0.67] Making Payments & Receiving [0.62] |
International [1.00] International business help [0.83] International Banking [0.80] |
Banking help [0.29] Accounts [0.25] |
Business Finance [1.00] Loan and Interest Rates [0.83] |
|
Small Business Advice Guide to starting a business Business advisory services Information about Kiwisaver Mobile Banking Application Features of internet banking Latest Economic Updates Business Banking Centre location
|
Payment Processing Times Fetch Recurring Payments Getting paid by direct debit Ways to pay a supplier Fees for using another banks ATMs What is a Visa Debit |
Exchange Rate Calculator Holding an Account in A Foreign Currency Receiving money from an international contact Paying someone overseas Managing risk when importing or exporting goods |
Getting an eftpos terminal Basic Business Account Descriptions |
Business Term Deposits Business Loans Asset finance Apply for a Business Credit Card Overdrafts Business Savings Account Interest Rate |
To visualize our clustering results in Table 1, we plotted the data in Figure 2. Figure 2 is designed to represent the relationships between cards in a multidimensional space. The cards are represented on a plot with Dimension 1 and Dimension 2 as axes. Dimensions are item attributes that seem to order the items in the map along a continuum. For example, an MDS of perceived similarities among breeds of dogs may show a distinct ordering of dogs by size. The ordering might go from right to left, top to bottom, or move diagonal at any angle across the map. At the same time, an independent ordering of dogs according to viciousness (or furriness, intelligence, etc.) might be observed. This ordering might be perpendicular to the size dimension or might cut a sharper angle. The underlying dimensions are thought to explain the perceived similarity between items. The relationship between the cards on the plot should represent their underlying dissimilarity. The cards that are located close to each other are perceived as being similar. In contrast, the cards that are positioned far away from each other indicate a large difference in perception. In fact, the cards closer together are more similar than those further apart. We made it clear that k-means clustering started from the partition that is obtained by hierarchical clustering for two-dimensional data points. Producing an IA of five cluster solutions in which each cluster is shown by different colors.

Figure 2. Multidimensional scaling of the clustering results in Table 1. Using two-dimensional data points produced a five-cluster solution with each cluster shown by different colors. Placing the cursor over any color ball point will highlight the two cards that the ball point represents.
Comparing Two- and Three-Dimensional Data Points
In order to evaluate the similarity and difference in the card sort data, we also applied k-means clustering by using three-dimensional data points to see how much the relationship between the cards and participants agreed with each other. Table 2 indicates the three-dimensional clustering results from the data shown in Figure 1. The names in each category were arranged according to their probabilities, and the cards were arranged in the order according to their distances from similarities to dissimilarities in each category. You can see that the clustering results on Table 2 have some new arrangements of cards and category names when compared to Table 1. Even though there are five k clusters, it is not of interest in card sorting. The participants agreed more with the clustering results in Table 2 than Table 1 based on the calculation of the category name probabilities. Clustering results from using two-dimensional data points produces a large number of clusters in comparison to three-dimensional data points when the number of participants and cards increases. A difference in cluster numbers illustrates the methodological issues with the choice of analysis for card sorting. We also visualize the clustering results of Table 2 in Figure 3 with each color representing a cluster. We repeated the test and found that it took around 3 to 6 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3. Note that we created our software tools to calculate and show the matrix in Figure 1. We also created our software tools to show the results in Table 1 and Figure 2.
Table 2. Best IA Submissions by Participants in the Card Sort Using Three-Dimensional Data Points from the Data Sets Given in Figure 1.
|
Cluster735 |
Cluster278 |
Cluster819 |
Cluster46 |
Cluster315 |
|
Information & Advice [1.00] Business Services & News [0.71] Useful information [0.62] |
Banking help [0.44] Accessing our Services [0.43] Administration [0.42] |
Payments [0.80] Using your accounts [0.71] Managing Payments [0.67] |
International [1.00] International business help [0.83] International Banking [0.80] |
Business Finance [1.00] Loan and Interest Rates [0.83] Helping your business grow [0.75] |
|
Business advisory services Information about Kiwisaver Guide to starting a business Small Business Advice Latest Economic Updates |
Getting an eftpos terminal Basic Business Account Descriptions Business Banking Centre Locations Features of internet banking What is a Visa Debit Card Mobile Banking Application |
Ways to pay a supplier Fees for using another banks ATMs Payment Processing Times Getting paid by direct debit Fetch Recurring Payments |
Holding an Account in A Foreign Currency Receiving money from an international contact Exchange Rate Calculator Managing risk when importing or exporting goods Paying someone overseas |
Asset finance Overdrafts Apply for A Business Credit Card Business Savings Account Interest Rate Business Term Deposits Business Loans |

Figure 3. Multidimensional scaling of the clustering results from Table 2. Using three-dimensional data points to produce five-cluster solutions in which each cluster is shown by different colors.
To validate the current algorithm, a comparison of the results with the predictions of other techniques of card sorting is provided in the next section.
Comparing Two- and Three-Dimensional Data Points with BMM, AAM, and PCA
In order to evaluate and compare the similarity and difference in the card sort data between the current algorithm and the Participant-Centric Analysis (PCA), Actual Agreement Method (AAM), and Best Merge Method (BMM), we need to understand each of those techniques first.
AAM and BMM
Dendrograms are used to visualize the results of a hierarchical cluster analysis and may provide insights into high-level topics (Righi et al., 2013). The AAM and BMM are derived from cluster analysis, and both techniques are widely used in the industry to see the patterns of users’ card sorting. AAM and BMM dendrograms analyze the participants’ responses and provides an interpretation of how the cards were categorized. It also displays how the results are generated depending on the algorithm that is used. In general, both techniques agree that the bigger the category, the more people will disagree with it. This means, as the number of cards in a category gets larger, it is less likely that multiple participants will have created that exact combination of cards. However, while many users can agree on very small categories, this is not a very useful result. Providing the full range of viable categories along with scores allows us to make an informed compromise between practical requirements and what the participants are telling us. In this study, the dendrogram displays the results of performing a cluster analysis on the similarity matrix and displays the result in a dendrogram format. The dendrogram shows card clustering from strong to weak and left to right. Hovering over any cluster circle will show the strength of that cluster as a percentage: 100% meaning all participants grouped those cards together and 50% meaning half of the participants placed those cards in the same group.
The AAM depicts only factual relationships and provides the most useful data if over 30 participants have completed your survey. The AAM algorithm counts each instance of a complete category from every participant. Each category with a non-zero score (a real category) inherits the base score (i.e., before inheritance) of all superset categories. The category with the highest score is taken, and all conflicting categories are eliminated. This algorithm works best with a lot of participants, but it generally provides better results compared to the BMM algorithm. The scores that AAM provides tells you X% of participants agree with this grouping See Figure 4 that shows the dendrogram results from the data sets from Figure 1. We repeated the test and found that it took around 3 to 5 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.

Figure 4. The AAM dendrogram. The percentage scale is at the top of the dendrogram. The scores show X% of participants who agree with a grouping. The thicker the lines, the more cards are merged together. The results are from the 15 participants who submitted valid results from 27 cards.
The BMM algorithm dendrogram makes the most of a smaller number of completed card sorts. The BMM breaks each instance of a category from every participant down to their base pairs. The pair with the highest score is locked in. This repeats, and where the pair being locked in intersects with an existing locked category, it is agglomerated with that category. All subsets of this new category are eliminated. The scores that BMM provide tells us X% of participants who agree with parts of this grouping. Figure 5 shows the dendrogram results from the data sets given in Figure 1.

Figure 5. The BMM dendrogram. The scores show the X% of participants who agree with this grouping. The thicker the lines, the more cards are merged together. The results are from the 15 participants who submitted valid results from the total of 27 cards. We repeated the test and found that it took around 3 to 5 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.
Participant-Centric Analysis (PCA)
PCA is a new method that was developed to show an alternative display of the card sort results. At a high level, the algorithm takes every participant’s IA and compares it to every other participant’s. The more cards that are sorted into the same sorts of clusters, the more agreement one IA will have with another. Once the algorithm is completed, and the IAs have all been compared, the most popular IA with the highest agreement across all the participants is displayed; this is the largest group of participants who created similar groups. The second IA is chosen from all the participants who weren’t supporters of the first IA, and so on. It treats all the participants as IAs and treats their submitted groups as votes. Table 3 shows the most popular IA that has the highest agreement across all the participants’ results from the data sets given in Figure 1.
Table 3. PCA: Best IA—7 out of 15 Participant Card Sorts Were Similar to this IA.
|
Business Overseas |
Business Finance |
Information & Advice |
Managing Payments |
Accessing our Services |
|
International Payments International Trading Doing business overseas |
Helping your business grow Loan and Interest Rates Setting up business accounts |
Business Services & News Business basics Things I might want to read once or at least not often |
Payments Business banking transactions Making Payments & Receiving |
Business banking |
|
Business advisory services Information about Kiwisaver Guide to starting a business Small Business Advice Latest Economic Updates |
Getting an eftpos terminal Basic Business Account Descriptions Business Banking Centre Locations Features of internet banking What is a Visa Debit Card Mobile Banking Application |
Latest Economic Updates Guide to starting a business Business advisory services Information about Kiwisaver Small Business Advice |
Payment Processing Times Ways to pay a supplier Getting paid by direct debit Getting an eftpos terminal Fetch Recurring Payments |
Fees for using another banks ATMs Features of internet banking Business Banking Centre Locations Mobile Banking Application |
Note: Includes results from the 15 participants who submitted valid results from 27 cards. We repeated the test and found that it took around 3 to 6 seconds to produce the results for the three-dimensional data points; these results are shown in Table 2 and Figure 3.
Comparison
These analyses for card sorting are chosen because all of them claim to determine a statistically optimal solution for website design. The analysis of the cards using AAM works by looking into whole clusters, rather than pairs. AAM provided better results of how participants agreed between each other, which could be transformed into meaningful steps for a website design.
In this study, we are looking for the most agreed IA. It can be seen that the AAM dendrogram result in Figure 4 provides many groups, but three of the groups contain a single card. Although many users can agree on very small categories, this is not a very useful result especially if categories are represented by a single card. Moreover, allowing a clustering algorithm to select a card that is distant from the rest of the data as an initial center, would produce poor results (Khan & Ahmad, 2004). The algorithms have direct impact on the formation of the final clusters. This can be seen with other techniques—when every cluster has at least two cards. By looking at a particular card, for example “Getting an eftpos terminal,” Figure 4 shows this as a single card in one of the group in AAM result. However, Figure 2 and 3 show that “Getting an eftpos terminal” has the coordinate (0.1815, -0.2320) in two-dimensional data points and coordinate (0.1815, -0.2320, 0.3139) in three-dimensional data points which are both close to more than one card. AAM provides more groups including groups that contain a single card when the technique uses large data sets. This will strengthen the dendrogram result to a more complex situation in order to determine the groups. The current approach discussed in this paper upgrades the results so that they are even more meaningful and easier to visualize and analyze.
The two-dimensional data points are a more likely visualization than the similarity matrix shown in the Figure 1 data. The arrangement of the cards in a cluster is more similar to what is shown along the right edge of the similarity matrix. Note that each cluster comprises the number of cards, and the order of the cards is arranged according to their distances from similarities to dissimilarities in each category. For example, Cluster881 and Cluster960 show the same arrangement of cards in each category as the similarity matrix does, which are highlighted with the dark blue color along the right edge. Cluster315 and Cluster46 in three-dimensional data points have the same number of cards and card names when compared to Cluster881 and Cluster960, but the order of the cards is varied. This is due to the calculation of the distance in three dimensions. Cluster590 in two-dimensional data points contains 8 cards as it can be seen at the top of the similarity matrix. In three-dimensional data points contains the same card names but reduced the number of cards to 5 in Cluster735. Both Cluster590 and Cluster735 contain two cards formed as a single card using the AAM algorithm as shown in Figure 4. One category in Figure 4 contains 3 cards (“Small Business Advice,” Guide to starting a business,” and “Business advisory services”) as shown in Cluster590 and Cluster735. The same category shown in Figure 4 appears further down on the similarity matrix to contain “Business Banking Center Locations.” This category arrangement does present some doubt about the efficacy of the AAM algorithm. The two single cards are next to this cluster and contain more agreements by participants. It can be seen that “Small Business Advice,” Guide to starting a business,” “Business advisory services,” “Information about Kiwisaver,” and “Latest Economic Updates” should be clustered together in Figure 1 as shown by the agreement in the two- and three-dimensional data points.
BMM is a technique based upon similarity matrixes. The limitation of BMM only works by merging the pairs, so it will be impossible to reconstruct this reduction. If we apply the threshold of 50% agreement to Figure 5, then we have five groups. Let’s compare one of the groups that contains similar cards as shown in Figure 5, Table 1, and Table 2. For example, Table 4 shows the result from one of the groups in Figure 5. This shows that five cards in Table 4 also appear in the category name “Information & Advice” in Table 2. The other two cards “Business Banking Centre Locations” and “Getting an eftpos terminal” in Table 4 are grouped differently in Table 2. To understand why the current algorithm clustered the two cards differently, we plot the result of Table 2 in Figure 6 viewing Dimension 3 as a function of Dimension 2. The green color circles in Figure 6 and 3 are the cards that contains in both BMM and k-mean algorithm for three-dimensional data points. Figure 6 shows “Business Banking Centre Locations” (0.1673, -0.1253, 0.0733) and “Getting an eftpos terminal” (0.2230, -0.0226, 0.0583) are both closer to the violet colored cluster than the green colored cluster. In two-dimensional data points, Table 1 shows that it contains all the cards in Table 4 in one cluster except one card “Getting an eftpos terminal.” In Figure 2, “Getting an eftpos terminal” is closer to another card than the rest of the cards in Table 4. This analysis indicates that the current approach can overcome the limitation of BMM by allowing the cards to reconstruct after a cluster is formed.
Table 4. One Group from Figure 5
|
Small Business Advice Guide to starting a business Business advisory services Information about Kiwisaver Latest Economic Updates Business Banking Centre Locations Getting an eftpos terminal |
The BMM method is known to work well with small sets of data, and it appears that BMM is driven well with two- and three-dimensional data points of data less than 30. Most of the categories in BMM contain cards similar to two- and three-dimensional data points categories more than in AAM categories. It can be seen that Cluster960 in two-dimensional data points and Cluster46 in three-dimensional data points have the same number of cards and card names with one category in BMM dendrogram in Figure 5. Figure 5 shows when the pair with the highest score is locked in, it will be impossible to reconstruct this reduction. This limitation is overwhelmed by two- and three-dimensional data points shown in Table 1 and 2. The card is arranged according to their distances from similarities to dissimilarities in each category.

Figure 6. Multidimensional scaling of the clustering results from Table 2 viewing from Dimension 2 against Dimension 3. Using three-dimensional data points, we produced a five-cluster solution in which each cluster is shown by different colors.
The result of two techniques (k-means algorithm and PCA) reveals that PCA results (Table 3) and three-dimension data points clustering results (Table 2) have more cards in the categories that are commonly compared to two-dimension data points clustering results (Table 1). The PCA best IA is chosen depending on the highest agreement across all the participants. This technique is understood to have weakness when the number of participants is small. For example, if a survey contains four participants, the PCA algorithm takes every participant’s IA and compares it to every other participant’s. If there is less agreement between the IAs then there is no popular IA that has the highest agreement across all the participants. The current algorithm overcomes this limitation and contributes to providing better and more meaningful results if a survey uses a small number of participants. Our approach can be easily used by any practitioners whether they are not familiar with MDS. They will only need to submit the data and leave it to the software to give the results.
The next section describes how the current algorithms handle overlapping and outliers.
Overlapping and Outliers
K-means algorithm uses two- and three-dimensional data points that are able to handle the overlaps quite well. Figures 2 and 3 show only 26 cards from the total of 27. The missing card is placed at the same position with another card. This is an overlap. We displayed the results in the basic layout showing all clusters and every card’s coordinates. The basic layout shows that two cards (“Small Business Advice” and “Guide to starting a business”) have the same coordinate of (0.26053, -0.23871, 0.32583). Observations of some data sets also show that some single cards are relatively distant from the rest of the data, known as outliers. In iterative clustering algorithms, the procedure adopted for choosing initial centers has a direct impact on the formation of final clusters. Our proposed algorithm allows the grouping of single cards with their closest core clusters treating outliers by choosing the strongest similarity cards from the similarity matrix. In future work, we may explore setting a threshold for this value. We also need to test and analyzes this approach in data for more than 50 cards and do more tests to overcome the limitation of the number of cards.
Conclusion
We have considered the combination of similarity matrix, k-means algorithm, and multidimensional scaling to cluster and calculate the most agreeable information architecture in card sorting data sets. The algorithm is applicable to any card sorting data sets, and it upgrades the results so they are meaningful and easier to visualize and analyze. We found that the participants’ card sorts agreed more with the clustering results when using the three-dimensional data points than the two-dimensional, based on the calculation of the category name probabilities.
The AAM dendrogram results provide many groups and contain categories with a single card. Although many users can agree on very small categories, this is not a very useful result especially if categories are represented by a single card. Moreover, allowing a clustering algorithm to select a card that is distant from the rest of the data as an initial center, would produce poor results. The algorithms will have direct impact on the formation of final clusters. Also the results analysis indicates that the current approach can overcome the limitation of BMM by allowing the cards to reconstruct after a cluster is formed. For PCA, the current algorithm contributes to providing better and more meaningful results if the survey uses a small number of participants. This method can work well in small card sorts of those less than 30 cards. Also, we will look very closely to the analysis cards of more than 30 and up to 100 cards. Our approach is also able to handle the overlaps and outliers quite well. The proposed clustering algorithms have been tested on real-world data sets and compared to other techniques.
Tips for UX Practitioners
The following are suggestions that UX practitioners can use in their own card sorting analysis:
- Use online card sorting tools to more easily convert data into a similarity matrix. The strongest pair is placed in the top left corner, grouping them with the next related strongest pair that either of those cards have, and then repeats the process for that new pair. This way, the algorithm attempts to cluster similar cards along the right edge of the matrix. Be careful if the similarity matrix presents both the upper and lower triangular together.
- Although most online tools do not provide the capability for users to group items into subcategories, this does not imply that this decision is any less important or should be varnished over quickly. The dendrogram provided in online tools can help you more easily make decisions about where large categories naturally break into subcategories.
- Save images while analyzing data especially during the rotation in three-dimensional images. These images are useful for future presentations, illustration of results, and for making decisions during the creation of information architecture.
- It is very important to look closely at the similarity matrix and compare with two- and three-dimensional data points. At the same time look at the AAM and the BBM results.
- Do not let the length or complexity of this process discourage you from performing it. Creating an IA is a critically important step in the design of a website or application. It forms the foundation of the user’s navigation experience. Time spent on ensuring the structure is as good as you can make it, based on user input, is time well spent.
- Do not be discourage if a card is not present at the MDS display. This shows that the overlapping process has occurred. You would know that these cards are placed together by clicking on each point or by looking at the coordinates display.
- This new methodology can be used by anyone, but those who will find it the most beneficial are when they have found that other methods produce hard to read results in the form of diagram. This new methodology can give the final result in groups, and also show a visualization of the results in two- and three-dimensions.
Acknowledgments
The authors are especially indebted to Andrew Mayfield and Keith Ng for the many valuable discussions of the problems to which the above results pertain. We also thank Optimal Workshop (http://www.optimalworkshop.com) for allowing this work to use their data and algorithms.
References
Abdi, H. (2007). Metric multidimensional scaling. In N. Salkind (Ed.), Encyclopedia of Measurement and Statistics (pp. 598–605). Thousand Oaks, CA, USA: Sage.
Arai, K., & Barakbah, A. R. (2007). Hierarchical k-means: An algorithm for centroids initialization for K-means. Reports of the Faculty of Science and Engineering, 36(1), 25–31.
Baker, K. (2005). Singular value decomposition tutorial. The Ohio State University.
Berry, M. W., Dumais, S. T., & Letsche, T. A. (1995). Computational methods for intelligent information access. In Proceedings of the 1995 ACM/ IEEE Supercomputing Conference, 1995.
Capra, M.G. (2005), Factor analysis of card sort data: An alternative to hierarchical cluster analysis, Proceedings of the Human Factors and Ergonomics Society 49th Annual Meeting, HFES 2005 (pp. 91–95). Santa Monica, CA: Human Factors an Ergonomics Society Inc.
Estivill-Castro, V. (2002). Why so many clustering algorithms: A position paper. ACM SIGKDD Explorations Newsletter, 4(1), 65–75.
Groenen, P. J., & Velden, M. (2014). Multidimensional scaling. John Wiley & Sons, Ltd.
Growe, G. A. (1999). Comparing algorithms and clustering data: Components of the data mining process (Doctoral dissertation, Grand Valley State University).
Hartigan, J. A., & Wong, M. A. (1979). Algorithm AS 136: A k-means clustering algorithm. Applied statistics, 28(1), 100–108.
Huang, Z. (1998). Extensions to the k-means algorithm for clustering large data sets with categorical values. Data mining and knowledge discovery, 2(3), 283–304.
Juran, J. M., & Godfrey, A. (1998). Quality control handbook. New York, NY: McGraw-Hill.
Kalbach, J. (2007). Designing web navigation: Optimizing the user experience. O’Reilly Media, Inc.
Kanungo, T., Mount, D. M., Netanyahu, N. S., Piatko, C. D., Silverman, R., & Wu, A. Y. (2002). An efficient k-means clustering algorithm: Analysis and implementation. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 24(7), 881–892.
Khan, S. S., & Ahmad, A. (2004). Cluster center initialization algorithm for K-means clustering. Pattern recognition letters, 25(11), 1293-1302.
Pawliczek, P., & Dzwinel, W. (2013). Interactive data mining by using multidimensional scaling. Procedia Computer Science, 18, 40–49.
Righi, C., James, J., Beasley, M., Day, D. L., Fox, J. E., Gieber, J., & Ruby, L. (2013). Card sort analysis best practices. Journal of Usability Studies, 8(3), 69–89.
Rosenfeld, L., & Morville, P. (2002). Information architecture for the world wide web. O’Reilly Media, Inc.
Spencer, D. (2009) Card sorting. Designing usable categories. Brooklyn, NY, USA: Rosenfeld Media.
Spencer, D., & Warfel, T. (2004, April 7). Card sorting: A definitive guide. Boxes and Arrows. Retrieved from http://boxesandarrows.com/card-sorting-a-definitive-guide/
Steward, G. (1993). On the early history of the singular value decomposition. SIAM Review, 25(4), 551–566.
Wood, J., & Wood, L. (2008). Card sorting: Current practices and beyond. Journal of Usability Studies, 4(1), 1–6.
Wu, X., Kumar, V., Quinlan, J. R., Ghosh, J., Yang, Q., Motoda, H., & Steinberg, D. (2008). Top 10 algorithms in data mining. Knowledge and Information Systems, 14(1), 1–37.
Wurman, R. S. (1996). Information Architects. Zurich, Switzerland: Graphis Inc.
Appendix: Transforming a Distance Matrix into a Cross-Product Matrix
In this approach, dissimilarities are treated as distances in space, and they must follow the rules that govern metric distance between cards. Specifically, the dissimilarity function d assigns to every pair of cards A and B a nonnegative number according to the following three axioms:
- d(A,B) ≥ d(A,A) = 0 is the dissimilarity between two cards is greater than or equal to the dissimilarity between a card and itself, which is zero;
- d(A,B) = d(B,A) is the dissimilarity of A to B is the same as the dissimilarity of B to A;
- d(A,B) + d(B,C) ≥ d(A,C) A and C cannot be farther apart in similarity space than the sum of their distances to any other object B.
If s is the similarity measure shown in Figure 1 that later ranges between 0 and 1 by normalizing using
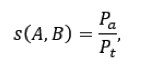
where is the number of participants that agree with each pair and the total number of participants. Then the corresponding dissimilarity measure can be defined as
![]()
In order to transform a distance matrix into a cross-product matrix, we use the approaches proposed by Abdi (2007), and the equation can be expressed in matrix form as:
![]()
where I is an identity matrix, U is an n by n matrix consisting entirely of 1s only and D is the distance matrix derived using Equation (1). The eigen-decomposition of this matrix gives
![]()
with and is the diagonal matrix of eigenvalues. Equation (3) is always achievable if we’re working with square symmetric matrix and we split into then Equation (3) becomes
![]()
One factoring technique we can use is called singular value decomposition (SUV; Baker, 2005; Berry, Dumais, & Letsche, 1995). As it turns out, the orthogonalization of a square symmetric matrix is a special case of SVD (Steward, 1993).
[:]
